

Mientras entre sus datos en la matriz, muévase de celda a celda usando la tecla Tab, no use la flecha o la tecla de entrada.
#QUADRATIC REGRESSION CALCULATOR SERIES#
Nota: Este JavaScript le facilita a usted realizar Análisis de Series Residuales, siempre y cuando usted introduzca variables independientes X en orden creciente. Introduzca hasta 84 pares de datos (X, Y), y luego presione el botón Calculate (Calcular.) Los espacios en blanco no son asumidos como ceros ni incluidos en los cálculos, pero los números cero si se incluyen. Misma inspección lo puede ayudar a determinar el modelo de regresión polinomial apropiado para ajustar sus datos. Si mediante una inspección visual al diagrama de dispersión no se puede rechazar la existencia de un comportamiento en “forma parabólica”, usted puede usar este JavaScript, de lo contrario, esta Proporciona modelos de regresión de parábola.Īntes de utilizar este JavaScript es necesario construir un diagrama de dispersión para sus datos. Modelos de regresiones Cuadráticos son normalmente usadas en áreas económicas tales como en la función de utilidad predicciones análisis de costo beneficio, etc. Regresión Cuadrática para el Ajuste de Modelos de Forma Parabólica The value of the curve occurs at co-ordinates: The gradient of the curve at any point is: The area bounded by the curve above the X-axis is: sq. They are written in the format ax 2+bx+c= y Thus every y value on the curve in Integral is equal to the sum of the area under the curve in function up to that point.ĭiagnostic Tools for Data Transformation DecisionsĪ quadratic is a curve of the parabola family. That is for X = 2, the area under the quadratic function curve between zero and 2 is: A = 3 (2) 3 -25 (2) 2 + 50 (2) = 24. For the integrated function above, the initial X value is zero and the ending X-value is whatever value we choose. It actually tells us the area between some beginning X-value and ending X-value (when we do what is called a definite integral). The integrated function tells us the net area under the curve function (between the function curve and the X-axis). If on the other hand we integrate our quadratic function, we obtain a new function (Y* = 3 X 3 - 25 X 2 + 50 X), which is graphed below. Thus at X = 2, the slope of the quadratic function is 18(2)- 50 = -14. The derivative function gives us the value of the slope (i.e., marginal value, rate of change) of our quadratic function at every point. If we take the derivative of our quadratic function, we obtain a new function, Y' = 18 X - 50, which is graphed next to the diagram of the function, 2. This function has a slope at every point. After editing, then click the "calculate" button.įor extensive edit or to use the JavaScript for a new set of data, then use the "clear" button.Ĭalculus of Quadratic Functions: The following is a very basic review of introductory calculus concepts using a quadratic function example: Y = 9 X 2 - 50 X + 50, which is graphed in following diagram. You may simply add a number to any blank cell, change a number to another in the same cell, or delete a number from a cell. To edit your data, including add/change/delete, you do not have to click on the "clear" button, and re-enter your data all over again.
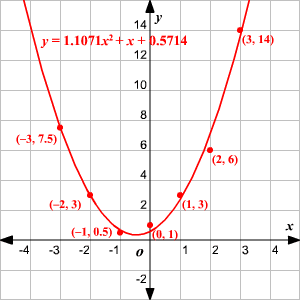
In entering your data to move from cell to cell in the data-matrix use the Tab key not arrow or enter keys. Notice: The JavaScript enables you to perform serial-residual analysis provided you enter the independent variable X in increasing order. Blank boxes are not included in the calculations but zeros are. Otherwise, visual inspection of the scatter-diagram enables you to determine what degree of polynomial regression models is the most appropriate for fitting to your data.Ī Typical Scatter-diagram for a Quadratic ModelĮnter your up-to-84 sample paired-data sets (X, Y), and then click the Calculate button. If by visual inspection of the scatter-diagram, you cannot reject a "parabola shape", then you may use this JavaScript. Prior to using this JavaScript it is necessary to construct the scatter-diagram for your data. This site also presents useful information about the characteristics of the fitted quadratic function. This JavaScript provides parabola regression model. Quadratic regression models are often used in economics areas such as utility function


 0 kommentar(er)
0 kommentar(er)
